RESEARCH
Forecasting Using Supervised Factors and Idiosyncratic Elements
(With Tae-Hwy Lee)
(With Tae-Hwy Lee)

[Paper]
Summary
We extend the Three-Pass Regression Filter (3PRF) by \cite{kelly} in two significant dimensions. First, we account for scenarios where the factor(s) may be weak. Second, we allow for a correlation between the target variable and the predictors, even after adjusting for common factors, driven by correlations in the idiosyncratic components of the covariates and the prediction target. Our primary theoretical contribution is to establish the consistency of 3PRF in estimating target-relevant factors under these broader assumptions. We show that these factors can be consistently estimated even when weak, though at a slower rate than strong factors. Importantly, we find that stronger relevant factors improve the rate of convergence of 3PRF to the infeasible best forecast relative to Principal Components Regression (PCR), with convergence rates increasing as relevant factors strengthen and slowing with stronger irrelevant factors. This highlights the theoretical superiority of 3PRF over PCR in terms of convergence—a novel result. Our second contribution is methodological: we introduce a Lasso step, forming the 3PRF-Lasso estimator, to model the target’s dependence on the idiosyncratic components of the predictors. We derive the rate at which the average prediction error from this step converges to zero, accounting for generated regressor effects. Extensive simulations indicate that 3PRF outperforms PCR under these modified assumptions, with significant gains from the Lasso step, even when only a few idiosyncratic components correlate with the target variable. In an empirical application, we use the 3PRF-Lasso framework to forecast key macroeconomic variables from the FRED-QD dataset, achieving robust performance relative to alternative methods across multiple horizons.
Working Papers
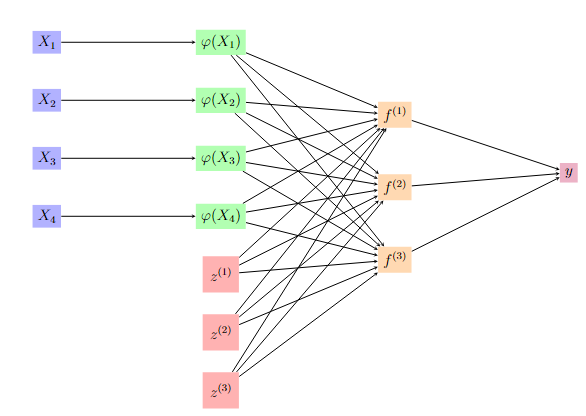
Kernel Three Pass Regression Filter
(with Rajveer Jat )
[Accepted for Presentation in The 2024 California Econometrics Conference ]
[Accepted for Presentation in The 34th Annual Midwest Econometrics Group Conference]
[Accepted for Presentation in European Winter Meeting of the Econometric Society (EWMES) 2024]
(with Rajveer Jat )
[Accepted for Presentation in The 2024 California Econometrics Conference ]
[Accepted for Presentation in The 34th Annual Midwest Econometrics Group Conference]
[Accepted for Presentation in European Winter Meeting of the Econometric Society (EWMES) 2024]
[Paper] [Poster]
Summary
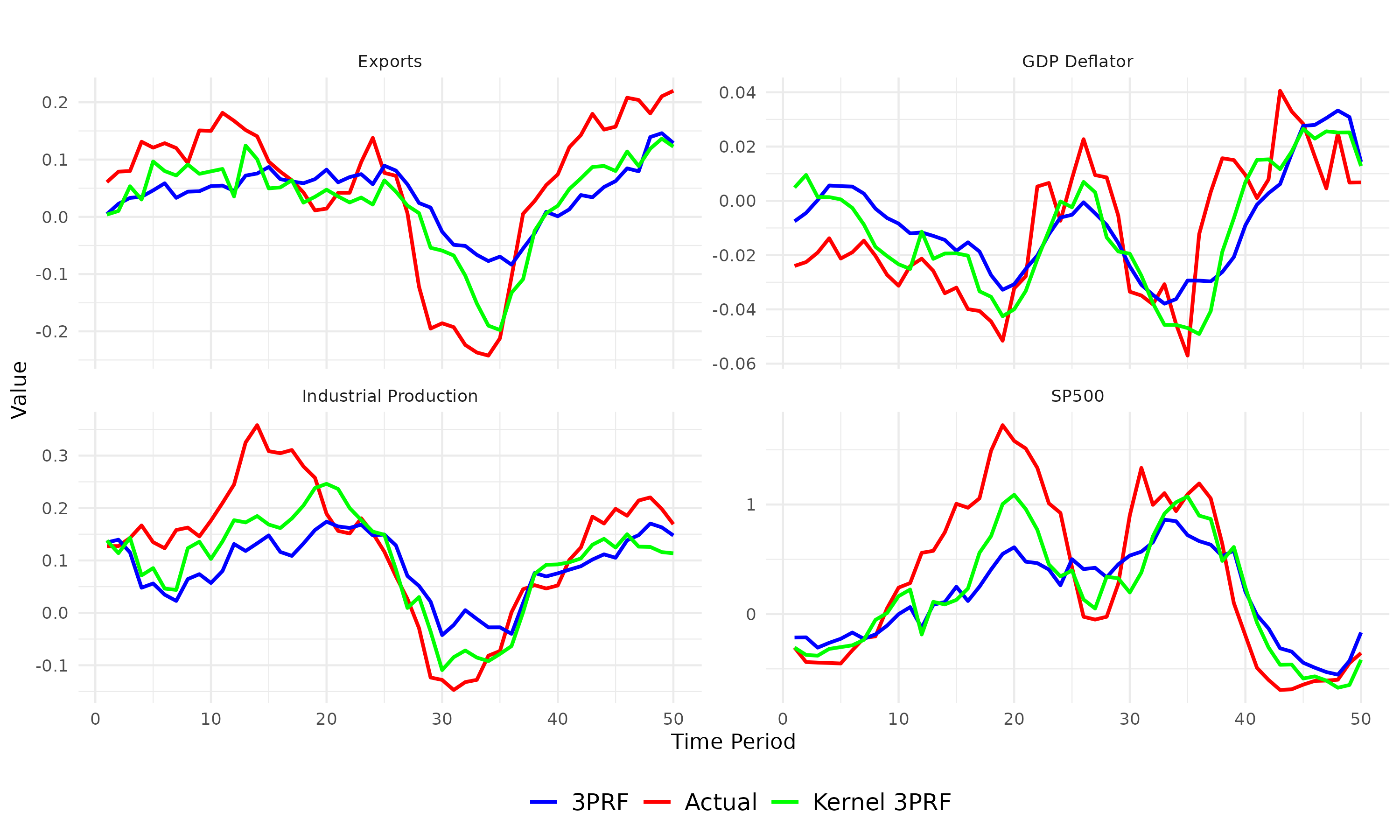
We forecast a single time series using a high-dimensional set of predictors. When predictors share common underlying dynamics, a latent factor model estimated by the Principal Component method effectively characterizes their co-movements. These latent factors succinctly summarize the data and aid in prediction, mitigating the curse of dimensionality. However, two significant drawbacks arise: (1) not all factors may be relevant, and utilizing all of them in constructing forecasts leads to inefficiency, and (2) typical models assume a linear dependence of the target on the set of predictors, which limits accuracy. We address these issues through a novel method: Kernel Three-Pass Regression Filter. This method extends a supervised forecasting technique, the Three-Pass Regression Filter, to exclude irrelevant information and operate within an enhanced framework capable of handling nonlinear dependencies. Our method is computationally efficient and demonstrates strong empirical performance, particularly over longer forecast horizons.
Weak Supervised Factors
Summary
This paper addresses scenarios where relevant factors exhibit varying strengths, in contrast to our first paper, which assumes uniform strength across all relevant factors. This extension is critical for capturing a broader range of real-world situations. For instance, when modeling a target with both local and global effects—such as the trajectory of returns for an automobile stock—a global factor may represent macroeconomic conditions affecting all stocks, while a local factor may capture sector-specific dynamics, such as fluctuations in automobile demand or supply. The existence of factors with differing strengths is well-documented in the literature, and we examine how this variability impacts forecasts generated by the Three-Pass Regression Filter (3PRF) estimator. Our findings reveal that variations in factor strength can render the 3PRF estimator inconsistent, serving as an important caution for researchers employing this supervised estimator. In the 3PRF framework, supervision occurs through the proxies, and we demonstrate that when factor strengths differ, these proxies must satisfy specific properties to ensure consistent forecasts—unlike the uniform strength case. In particular, we show that to consistently estimate weaker factors, there must exist certain proxies that are primarily influenced by these weak factors and only minimally by stronger factors. This result warns against the arbitrary usage of proxies, emphasizing that linearly independent loadings alone are insufficient for achieving consistency when factor strengths vary, a departure from the uniform strength scenario. Additionally, we show that the 'auto-proxy' procedure—used to construct proxies from the target variable—can generate proxies that meet these new requirements. Under certain conditions regarding the relative strengths of factors, the loading matrix of the auto-proxies assumes an asymptotic lower triangular structure, allowing for consistent estimation of both factors and the target. This result provides valuable insights into the well-known Partial Least Squares (PLS) method, given the close relationship between the auto-proxy 3PRF and PLS. The structural similarities between the two methods suggest that the conditions identified for consistent factor estimation in the 3PRF framework can also inform the application of PLS, particularly when dealing with factors of varying strengths.
Work In Progress
Supervised Instruments in a Data-Rich Environment
Summary
This paper investigates the estimation of a causal parameter in the presence of many instruments, building on the framework proposed by Bai (2010). We consider a scenario where both the endogenous regressors and the instruments are driven by a few common factors. In such cases, using a large set of instruments can render the conventional two-stage least squares (2SLS) estimator inconsistent. However, the factor structure enables us to derive a smaller set of instruments, restoring the consistency of the 2SLS estimator. Our paper introduces several key innovations. First, we allow the factors driving the endogenous regressors to be a strict subset of the factors driving the larger set of instruments. This refinement enables a more efficient estimator compared to the one in Bai's framework. Additionally, we account for the possibility of weaker underlying factors, leading to weak instruments. Under certain conditions, which depend on the strength of both relevant and irrelevant factors, we demonstrate that inference on the causal parameter β can proceed as if the true instruments were observed. Specifically, the estimation error in the factor estimation process does not affect the asymptotic variance of the causal parameter.
Summary
We use a neural network to forecast a single time series. Inspired by the "Targeted Predictors" approach from Bai (2008), we first select a set of predictors by performing polynomial regression for each predictor individually. Unlike traditional factor models, which limit the search to an underlying planar structure, our approach explores a non-linear, low-dimensional representation of the predictors which best explain y.